入力ベクトル(入力層のニューロン の集まり)を
,出力ベクトル(出力層のニューロン
の集まり)を
とする.また,この2つの層間の重みを表す行列を
,バイアスを
とする.行列
の構成要素は以下のようにインデックスを振る.
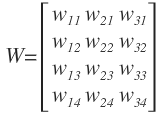
行列内要素 は,入力層の
番目のニューロンから出力層の
番目のニューロンへの重みを表す.
入力層と出力層のみからなる超シンプルなニューラルネットワークは下の図のように描ける.今回は出力層と設定した層内のそれぞれのノードの入力に対して活性化関数を作用させて次の層に繋いでいこうと考えれば,これを中間層として扱うこともできる.
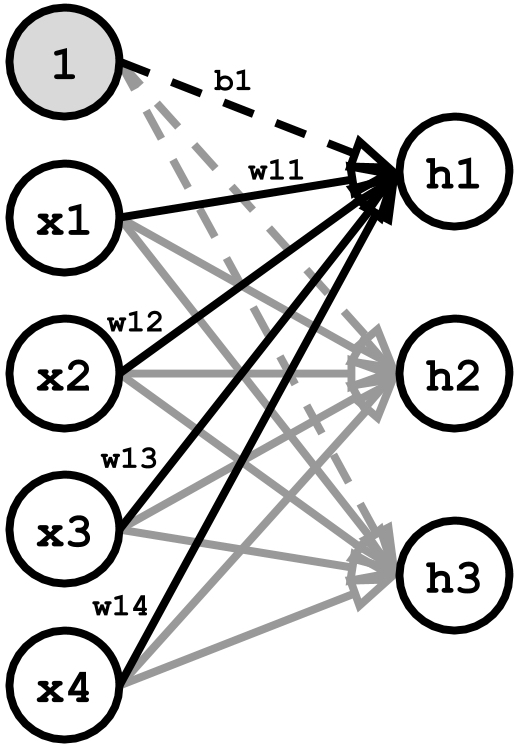
入力層の各ニューロンに与えられた値は,重みを掛けてバイアスを足されて,次の層に反映される.出力層内のある1つのニューロン を見てみると,これに対する入力は次式のように書ける.
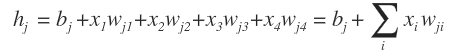
出力層のノード に関してこのような計算を行えば,出力ベクトル
を求めることができる.この計算がやっていることは,「入力ノードの値と対応する重みを掛けて,最後にバイアス項を足す」という処理を繰り返しているだけなので,以下のように行列の内積演算の形で立式することもできる.
$$ H = X \cdot W + B $$
これは高校数学で言うと, の形の行列と
の形の行列の内積を解いて,おまけにもう1つの行列を足すという問題になる.高校生の頃は「内積するもの同士の行と列の要素数を揃えて...」くらいのことしか考えていなかったので,当時に上のネットワークのようなイメージが描けていたらもっと楽しかったのだろうなと思う.
PythonでNumPyを使ってプログラムを書くときも,出力ノード に関するforループを回すよりもNumPyの内積演算を利用したほうが高速に解ける.
import numpy as np H = np.dot(X, W) + B