ゼロから作るDeep Learningの第3章あたりの話.3章の内容は何回かに分けて書きます.
活性化関数
下の図では,とあるノードに3つの入力 が与えられていて,これらの入力に基いて1つの出力値
が決定されている.このように,ノードへの入力の和を引数にとり,それに応じたノードの振る舞いを決める関数を活性化関数
という.
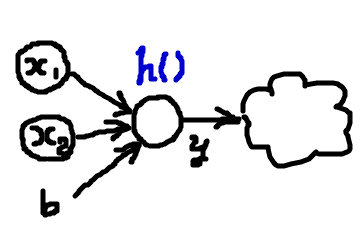
つまり,ノードで起きていることを数式で表現すると
$$ y = h(b + \sum_{i} w_i x_i) $$
となる.非線形な活性化関数 をいろいろ変えることによってニューラルネットワークを構築できる.以降で紹介する関数の図は横軸が
の引数で,縦軸が
を表している.
ステップ関数
- 引数(ノードへの入力の和)が0以下であれば0を返し,引数が正であれば1を返す.
- パーセプトロンで使われている活性化関数
$$ h(x) = \begin{cases} 0 & x \le 0\\ 1 & x > 0 \\ \end{cases} $$
def step_function (x): return np.array(x > 0, dtype=np.int)

シグモイド関数
- ニューラルネットワークでよく用いられる活性化関数
- ステップ関数と異なって,出力は連続値をとる.出力値が0, 1のどちらかではなくて,どれくらい0, 1に近いのかを示すことができるため,パーセプトロンよりも表現力が高いネットワークを構成できる
- どのような大きさの引数をとっても,出力値
が
に抑え込まれる点はステップ関数と共通している
- 値域が
の範囲において,接線の傾きが0になる点
がないことも重要なポイント
$$ h(x) = \frac{1}{1 + exp(-x)} $$
def sigmoid (x): return 1 / (1 + np.exp(-x))

ReLU関数(ランプ関数)
- Rectified Linear Unit 関数
- 引数(ノードへの入力の和)が0以下である場合は0を返し,引数が正であればそのままの値を返す.
- 引数が負であるときの挙動はステップ関数と同じ.引数が正の場合に,1を返すのではなく,受け取った値をそのまま返却しているところがパーセプトロンと異なる.
- sigmoid関数よりも後に登場した関数で,よく用いられているらしい.
$$ h(x) = \begin{cases} 0 & x \le 0\\ x & x > 0 \\ \end{cases} $$
def relu (x): return np.maximum(0, x)

Maxout関数
- Deep Learningと画像認識 ~歴史・理論・実践~ というスライドで知った
- 比較的新しめの活性化関数
- 始点となる層と,接続されている次のノードとの間に,
個のノードから成るプチ中間層みたいなものを作る.始点となる層とプチ中間層で内積を計算して,プチ中間層内での最大値を接続先のノードの出力値とする.
- 数式で書き下す Maxout Networks の図と解説が分かりやすい